Matteo Anderloni per lavoro analizza grandi rischi, gli abbiamo chiesto di spiegarci come si tratta il rischio e come viene percepito. Bastano poche basi teoriche per capire come istinto e razionalità non vadano d’accordo, e come la mente umana percepisce il rischio in maniera distorta.
Le soluzioni non sono semplici da elaborare, ma non è impossibile con le giuste conoscenze.
A cura di Francesco Chirico
Come si analizza il rischio a livello scientifico?
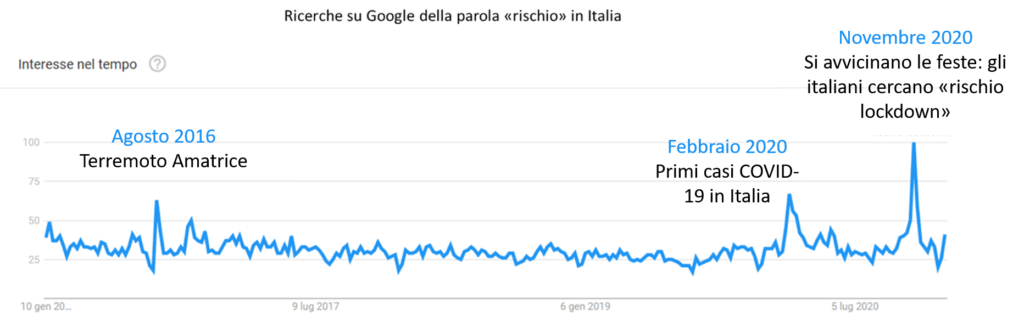
Il termine rischio è diventato di estrema rilevanza nell’ultimo periodo grazie, si fa per dire, alla diffusione del coronavirus. Basti pensare che le ricerche su Google contenenti questo termine nella prima settimana di novembre scorso sono aumentate del 225% rispetto alla media dei due anni precedenti. Gli unici picchi simili, ma comunque inferiori, negli ultimi 5 anni sono del febbraio scorso in seguito alla rilevazione dei primi casi italiani di Covid19 e ad agosto 2016 in concomitanza con il terremoto di Amatrice.
Per affrontare al meglio tutte queste dinamiche complesse, i politici, chi si occupa di comunicazione, ma anche ognuno di noi dovrebbe conoscere questa parola non solo dal punto di vista letterario ma anche dal punto di vista tecnico-scientifico.
Sappiamo con quale unità di misura si esprime il rischio? Sappiamo paragonare, quantitativamente, due rischi molto differenti tra loro? Pensiamo ad esempio al tema degli effetti collaterali dei vaccini. Esistono, è importante conoscerli, ma è altrettanto importante commisurarli: è più rischioso fare un vaccino o attraversare la strada?
Dal punto di vista quantitativo il rischio R viene espresso come il prodotto tra due fattori1:
R = P x D
Con P si indica la pericolosità cioè la probabilità che si verifichi un certo evento. In ambito catastrofale, spesso viene indicata come l’inverso del tempo ritorno, inteso come il tempo medio che intercorre tra due eventi simili.
Con D si indica semplicemente il danno atteso. È la variabile che determinerà dimensionalmente il rischio. Possiamo esprimerla in termini di vite umane, di superficie costruita o con qualsiasi altra unità di misura che ci interessi monitorare. Solitamente, sia per bieche ragioni capitalistiche che per poter confrontare rischi diversi tra loro, viene espressa in termini economici.
Grazie alla semplice equazione che abbiamo descritto è possibile misurare il rischio di un qualsiasi evento e rappresentarlo nel piano cartesiano D-P. Ricordando che R = D x P è facile dimostrare come il rischio associato ad un evento è pari all’area del rettangolo che ha per altezza la probabilità di occorrenza e per base il danno atteso associato all’evento stesso.
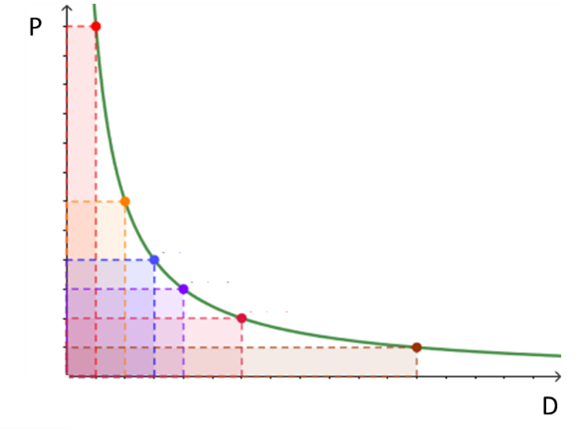
Intuitivamente un evento molto frequente ma con danno atteso basso, è rappresentato da un rettangolo con base stretta ma altezza elevata. Un evento raro ma con danno atteso elevato è rappresentato viceversa da un rettangolo con base elevata e altezza ridotta. Le due aree possono essere uguali e, pertanto, rappresentare lo stesso livello di rischio. Estendendo questo ragionamento a infiniti rettangoli è possibile raffigurare un livello di rischio costante come un ramo di iperbole; infatti i rettangoli associati ad ogni punto dell’iperbole hanno stessa area.
Se fissiamo una soglia di rischio accettabile, chiamata Ra, qualunque sia il suo valore, possiamo identificare nel piano DP due regioni: una che è l’insieme dei punti con R>Ra e l’altra dove R<Ra.
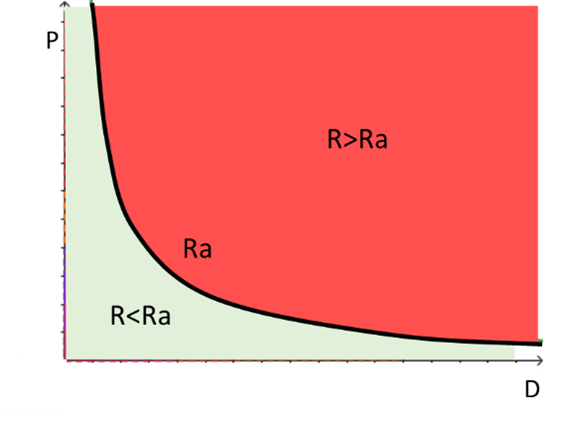
Se l’uomo fosse un individuo perfettamente razionale (spoiler: vedremo in seguito che non è così), tutti i rischi appartenenti alla regione rossa sarebbero non accettabili, al contrario dei punti della regione verde, e questo accadrebbe indipendentemente dal valore di D e di P.
Si può modificare il rischio?
È possibile intervenire e modificare il rischio associato ad un evento cercando di spostarlo dalla regione rossa a quella verde.
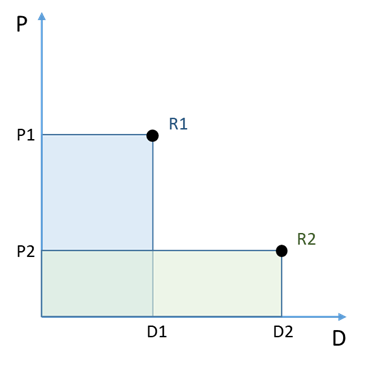
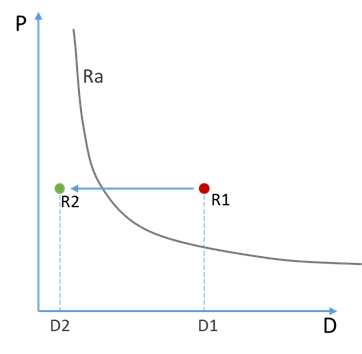
Proviamo ad aiutarci con un esempio: pensiamo ad una casa costruita in prossimità di un fiume soggetto ad esondazioni. Per proteggere la casa è possibile costruire delle barriere attuando così quello che è un intervento di protezione: in questo caso non si interviene sulla probabilità del fiume di esondare ma si agisce direttamente sul danno atteso in caso di esondazione diminuendolo da un livello D1 a un livello D2. Gli interventi di protezione, diminuendo il danno atteso, hanno l’effetto di spostare la curva di rischio da un punto R1 ad un punto R2 posto alla sua sinistra.
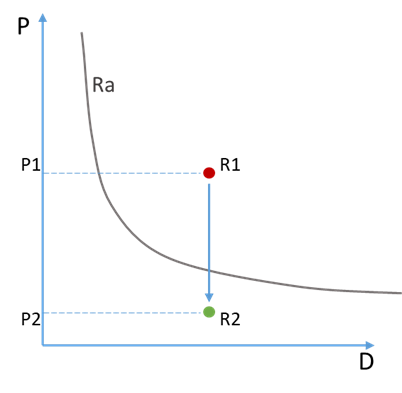
Un altro metodo potrebbe essere quello di agire sulla probabilità che avvenga l’alluvione intervenendo ad esempio sulla pulizia e sulla manutenzione dell’alveo: in questo caso si parla di interventi di mitigazione. Le opere di mitigazione spostano le curve di rischio verso il basso, diminuendo la probabilità di accadimento da P1 a P2.
È possibile agire sul rischio anche con meccanismi di mutualità come la disposizione di indennizzi statali o attraverso coperture assicurative. Interventi di questo genere non modificano il rischio totale in quanto non intervengono fisicamente sull’evento, ma impattano la forma della curva di distribuzione del rischio: a fronte di un pagamento sicuro contenuto (le tasse o il premio assicurativo) riduciamo un elevato danno poco probabile (la perdita in caso di evento avverso).
È importante notare come alcuni interventi possano diminuire il rischio per alcuni eventi ma aumentarlo per eventi simili. Tornando all’esempio dell’esondazione, la costruzione di una diga o l’innalzamento artificiale degli argini può diminuire la probabilità di piccole esondazioni ma aumentare esponenzialmente il danno atteso in caso di un crollo degli stessi.
Quanto è complesso quantificare il rischio?
Alcuni di voi potrebbero chiedersi come mai se l’equazione che permette di misurare un rischio è piuttosto semplice, trattandosi di fatto del semplice prodotto di due fattori, sia così complesso comprendere, quantificare e gestire i rischi.
La risposta a tale quesito è da ricercare in due fattori distinti.
Il primo è di carattere scientifico-matematico. I fenomeni per i quali è più interessante misurare il rischio sono caratterizzati da due fattori: sono caotici e rari. La natura caotica dei fenomeni catastrofali rende complesso stimarne la probabilità, in quanto ogni piccola variazione nel sistema iniziale produce importanti variazioni nel sistema finale. La rarità dei fenomeni si traduce in una piccola quantità di dati a disposizione con effetti importanti sugli errori di stima. E se calcolare la distribuzione di probabilità di un fenomeno di questo genere è complesso, probabilmente è ancora più difficile stimarne il danno atteso. La società sempre più dinamica e la complessità delle relazioni strutturali delle comunità rende difficile calcolare con esattezza tutti gli effetti diretti e indiretti associati ad un fenomeno. Questo aspetto non deve, però, scoraggiarci: gli scienziati hanno sviluppato negli anni modelli tanto complessi quanto solidi per stimare il rischio per centinaia di scenari distinti. Tocca a noi, intesi come comunità, l’onere di sfruttare al meglio queste informazioni per individuarne le priorità e sviluppare piani di protezione e prevenzione adeguati.
Il secondo fattore ha carattere profondamente umano. Per millenni l’homo sapiens ha basato la propria sopravvivenza sull’istinto. Ma sappiamo che istinto e razionalità non sempre vanno d’accordo, questo accade ancora più di rado quando di mezzo c’è la statistica. Se così non fosse non esisterebbe il gioco d’azzardo.
Alcuni studi hanno evidenziato diversi meccanismi che ci impediscono di valutare in maniera lucida e razionale il rischio. In alcuni casi intervengono, ad esempio, dinamiche di overconfidence che ci portano a sottovalutare rischi che dipendono direttamente da noi o ai quali ci sottoponiamo volontariamente. Uno dei fenomeni più importanti è quello che ci porta a sottovalutare i rischi frequenti ma con un danno limitato rispetto a rischi rari ma catastrofici: questo pensiero ci porta a percepire un viaggio in aereo come più rischioso di uno in automobile o ci porta, in maniera provocatoria, ad opporci con forza alla costruzione di un termovalorizzatore, ma non ci impedisce di fumare.
Infine, la nostra percezione di un rischio è tanto elevata quanto più esso è vicino nel tempo: ogni terremoto che ha colpito il Paese ha acceso l’attenzione sul tema del rischio sismico e altrettanto prontamente è stato riposto nel cassetto dopo poche settimane. O ancora, il Covid19 ha, giustamente, smosso risorse economiche e organizzative mai viste prima portandoci a cambiare la nostra quotidianità per mesi. Facessimo un centesimo dello stesso sforzo per affrontare i cambiamenti climatici…
[1] Tale definizione è valida sotto le ipotesi di probabilità disgiunta e invarianza temporale del valore esposto e della vulnerabilità. Nel caso più generale il Rischio è definito come l’integrale di convoluzione tra la Pericolosità, il Valore Esposto e la Vulnerabilità.